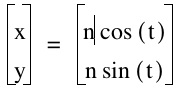Write Up 10: Parametric Equations
Introduction:

A parametric curve in the plane is a pair of functions:
x=f(t)
y=g(t)
where the two continuous functions define ordered pairs (x , y). In this write, we will be discussing the parametric equations x=acos(t) and y=bsin(t). We will mainly be exploring graphically what happens to a parametric equation with various values of the variables "a" and 'b." Throughout the write up, we will look at many different cases when discussing different values for "a" and "b".
Case 1: Both "a" and "b" are greater than zero ![]() [a,b>0]
[a,b>0] ![]() More specifically {a=b}
More specifically {a=b}
Lets assign arbitrary values for our variables: a=1 and b=1 (See graph below)
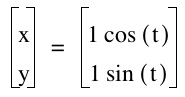
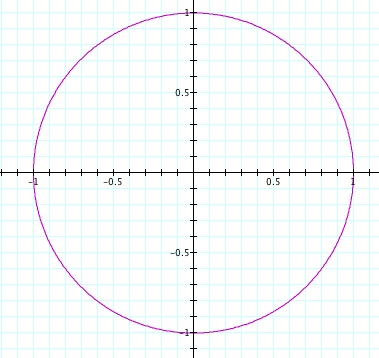
Observe that our values for our variables are the points where the circle crosses the x-axis and the y-axis. Therefore, we can conclude that when a=b, the value for a & b will be the length of the radius of the circle created by the parametric equation.
Let's look at another example to check our theory Suppose a=2 and b=2 (See graph below)
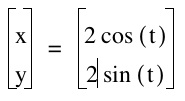
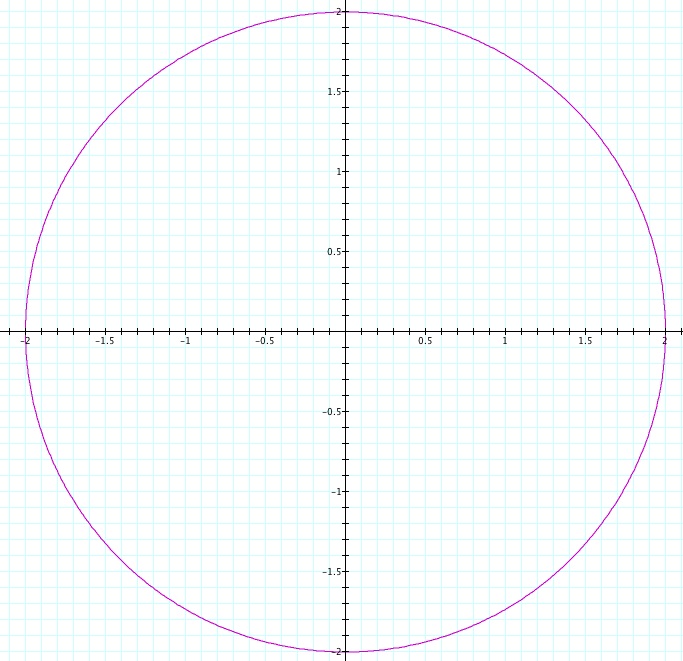
Hence, our theory holds when the values of "a" and "b' both equal 2. We can see in the graph above that the radius of the circle created by the parametric equations is a length of 2; which again is the values of our variables a & b.
Subcase 2: Both "a" and "b" are greater than zero ![]() [a,b>0]
[a,b>0]![]() More specifically {a
More specifically {a![]() b}
b}
Lets assign arbitrary values for our variables: a=2 and b=3 (See Graph Below)
Interestingly, when a
b the parametric equation no longer produces a circle but rather a elipses Also the specific values of our variables "a" and "b' have a direct relationship to the points of intersection of where the elipses crosses both the x-axis and the y-axis. By looking at the graph, we can see that the elipses crosses the x-axis at x=2 and x= -2. This tell us that the value of a=2 is the length of the radius of the elipses along the the x-axis. Also by looking at the graph, we can see that the elipses crosses the y-axis at the y=3 and y=-3. This tells us that the value of b=3 is the length of the radius of the elipses along the y-axis. Therefore, we can make the claim that for the values of "a" and "b" given that they are not equal, will give us the points in which the elipses crosses the corresponding axis. More specifically, the value of "a" will tell us the x-intercepts of the elipses and the values of "b" will tell us the y-intercepts of the elipses Let's check our claim with some new values for "a" and "b."
Let's switch the values of "a" and "b": Suppose a=3 and b=2
Hence, our claim is correct. The value for the variable "a" tell us the values of the x-intercepts of the elipses. Also the value of the variable "b" tell us the values of the y-intercepts of the elipses.
Subcase 2: Both "a" and "b" are less than zero ![]() [a,b < 0]
[a,b < 0]![]() More specifically {a=b}
More specifically {a=b}
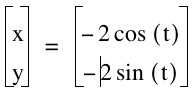
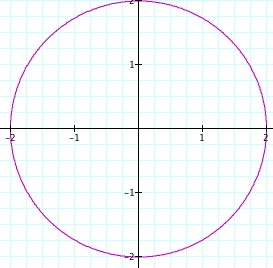
From the graph, we can make the conclusion that the sign of the values of the variables "a" and "b" do not affect the graph of the parametric equation. Therefore we can make the conclusion that the values of "a" and "b" are magnitudes. Hence, radii cannot be negative and therefore, whatever the numerical value of the variables "a" and "b" will tell us the x&y-intercepts for the circle or elipsis depending on whether or not a=b or a
b.
One Last Look:
Lastly, let's observe the parametric equation as our variables "a" and "b" vary: